2017/09/11
2020/05/05
掃き出し法を用いた逆行列の求め方
当ページでは、掃き出し方を使って逆行列を求める方法や実際に逆行列を求める手順を各ステップごとに丁寧に解説しています。
逆行列の求め方には、余因子行列を用いた方法もあり、そちらは余因子行列を用いた逆行列の求め方と例題に詳細に記載しました。臨機応変に簡単だと思われる方を選択して、楽に解きましょう!
掃き出し法とは
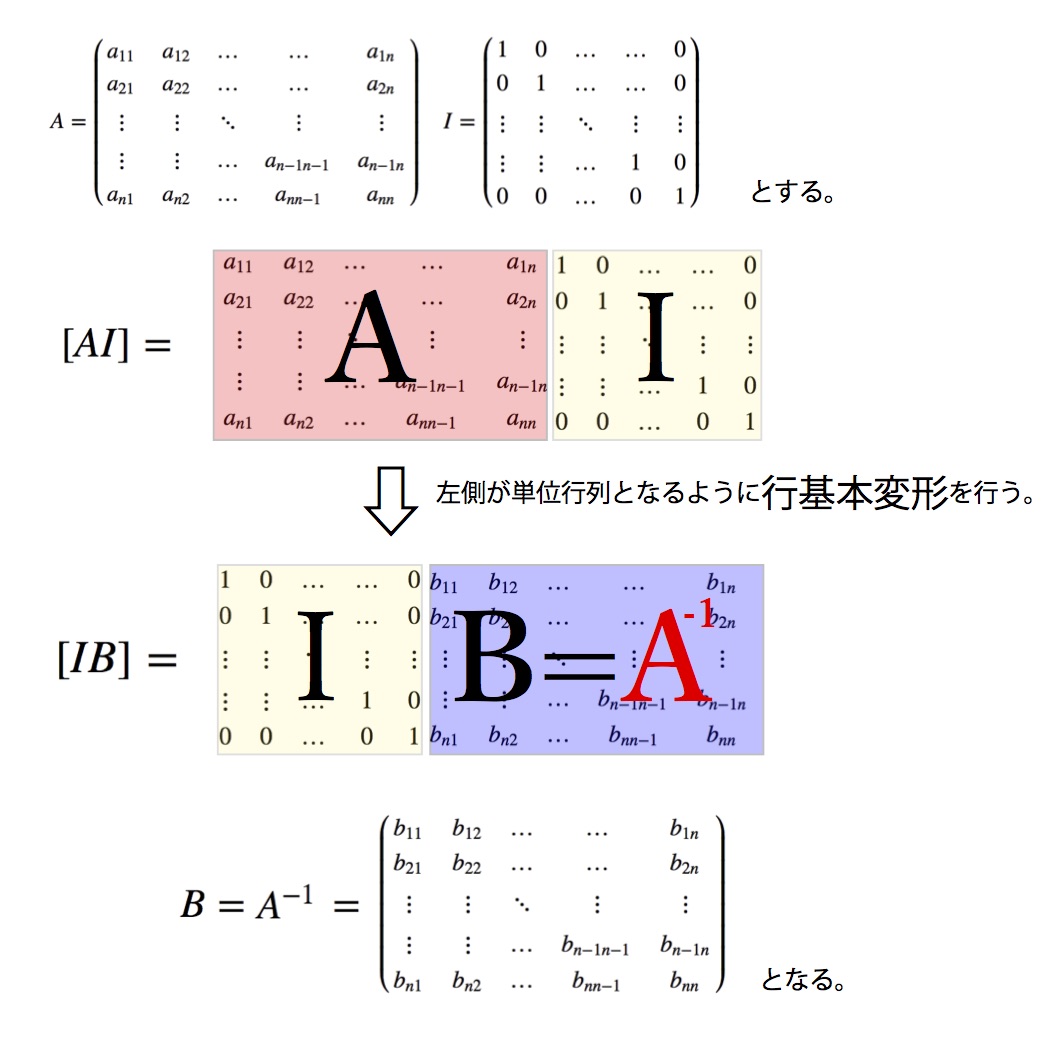
行列Aの右隣に単位行列Iをつけ、行基本変形を行い、[I B]に変形する。
この行列Bが行列Aの逆行列\(A^{-1}\)となる。
\(n×n\)行列の掃き出し法
例題
行列\(A= \begin{pmatrix}1 & 2 & 2 \\ 0 & 1 & 2 \\ 2 & 1 & 1 \end{pmatrix}\)の逆行列\(A^{-1}\)を求めよ。
回答
行列Aの右隣に単位行列Iをつけ、\( \begin{pmatrix}1 & 2 & 2 & 1 & 0 & 0 \\ 0 & 1 & 2 & 0 & 1 & 0 \\ 2 & 1 & 1 & 0 & 0 & 1 \end{pmatrix}\)とし、この行列を行基本変形し、[I B]の形になるように意識しながら変形します。
まず、この行列の1行目を-2倍し3行目に加えると次のようになる。
\( \begin{pmatrix}1 & 2 & 2 & 1 & 0 & 0 \\ 0 & 1 & 2 & 0 & 1 & 0 \\ 0 & -3 & -3 & -2 & 0 & 1 \end{pmatrix}\)
次に2行目の行列の-2倍を1行目に加え、3行目の行列に\(-\frac{ 1 }{ 3 }\)をかけると次のようになる。
\( \begin{pmatrix}1 & 0 & -2 & 1 & -2 & 0 \\ 0 & 1 & 2 & 0 & 1 & 0 \\ 0 & 1 & 1 & \frac{ 2 }{ 3 } & 0 & -\frac{ 1 }{ 3 }\end{pmatrix}\)
同様に2行目の行列の-1倍を3行目に加えると次のようになる。
\( \begin{pmatrix}1 & 0 & -2 & 1 & -2 & 0 \\ 0 & 1 & 2 & 0 & 1 & 0 \\ 0 & 0 & -1 & \frac{ 2 }{ 3 } & -1 & -\frac{ 1 }{ 3 }\end{pmatrix}\)
同様に3行目の行列の-2倍を1行目に加え、3行目の行列の2倍を2行目に加えると次のようになる。
\( \begin{pmatrix}1 & 0 & 0 & -\frac{ 1 }{ 3 } & 0 & \frac{ 2 }{ 3 } \\ 0 & 1 & 0 & \frac{ 4 }{ 3 } & -1 & -\frac{ 2 }{ 3 } \\ 0 & 0 & -1 & \frac{ 2 }{ 3 } & -1 & -\frac{ 1 }{ 3 }\end{pmatrix}\)
最後に3行目を-1倍かける。
\( \begin{pmatrix}1 & 0 & 0 & -\frac{ 1 }{ 3 } & 0 & \frac{ 2 }{ 3 } \\ 0 & 1 & 0 & \frac{ 4 }{ 3 } & -1 & -\frac{ 2 }{ 3 } \\ 0 & 0 & 1 & -\frac{ 2 }{ 3 } & 1 & \frac{ 1 }{ 3 }\end{pmatrix}\)
以上より、[I B]の形に式変形することができました。よって
\( A^{-1}=\begin{pmatrix} -\frac{ 1 }{ 3 } & 0 & \frac{ 2 }{ 3 } \\ \frac{ 4 }{ 3 } & -1 & -\frac{ 2 }{ 3 } \\ -\frac{ 2 }{ 3 } & 1 & \frac{ 1 }{ 3 }\end{pmatrix}\)
となります。
COMMENT
-
鈴木開智 2018.5.28 5:08 PM
答えに誤りがありませんか?1行3列目の答えです。
-
y0he1 2018.5.31 7:26 PM
ご指摘ありがとうございます。おっしゃる通りです。
\(\frac{1}{3}\)ではなく、\(\frac{2}{3}\)でした。
途中式も含めて修正させていただきました。













鈴木開智 2018.5.28 5:08 PM
答えに誤りがありませんか?1行3列目の答えです。
y0he1 2018.5.31 7:26 PM
ご指摘ありがとうございます。おっしゃる通りです。
\(\frac{1}{3}\)ではなく、\(\frac{2}{3}\)でした。
途中式も含めて修正させていただきました。